TensorFlow学习笔记（二）：优化方法

常见的一些神经网络训练更新方法

本文提到的方法：

Stochastic Gradient Descent (SGD), 随机梯度下降法

Momentum，惯性(动量)法

AdaGrad，适应性(Adaptive)梯度法

RMSProp，root mean square prop，均方根传播法

Adam，适应性惯性法

1. SGD方法

SGD方法是一种耗时较长的更新方法，在实际应用上可以分为batch、mini-batch和stochastic三种方式，但实际上用到的数学方法是一致的：

\[g_t = \nabla_{\theta_{t-1}}f(\theta_{t-1})\] \[\Delta\theta_t = - \eta * g_t\]

这里的$\theta_{t-1}$指的是上一次训练的参数，$f()$为损失函数，$g_t$就是损失函数的梯度，$\eta$是学习率

batch：用整个训练集训练一次后再计算损失函数的梯度
mini-batch：将训练集拆分成若干子集，计算损失函数的梯度，速度快，这是目前主流的方法
stochastic：每读入一个数据就马上计算梯度来更新参数

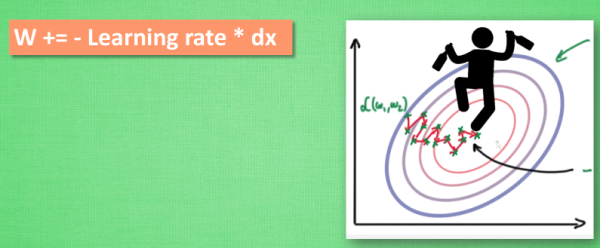
2. Momentum方法

SGD的衍生，模拟动量的概念，通过累积动量来替代真正的梯度:

\[m_t = \mu * m_{t-1} + g_t\] \[\Delta\theta_t = - \eta * m_t\]

其中$\mu$为动量因子。

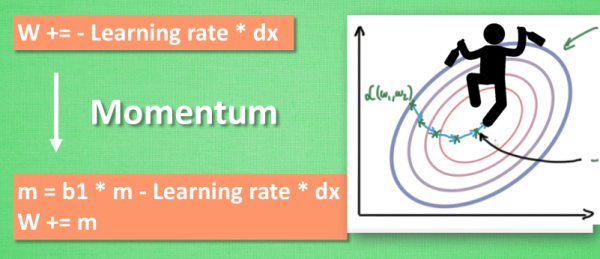
因为不断累积的$m_t$会影响下降的方向，相比SGD方法，动量法的优点是梯度下降方向更稳定，收敛速度更快，而选取不同的$\mu$值也很容易改变动量的影响程度。

3. AdaGrad

上述方法有一个特点是它们的学习率都是固定的，而AdaGrad方法可以在每轮训练中对每个参数的学习率进行更新：

\[n_t = n_{t-1} + g^2_t\] \[\Delta\theta_t = - \frac{\eta}{\sqrt{n_t + \epsilon}} * g_t\]

$\epsilon$为一常数用于避免分母为0。可以看出，对于较大的$g_t$，其实际学习率会比较低。

缺点是在中后期，$n_t$会越来越大，使得$\Delta\theta_t \rightarrow 0$，使得训练提前结束。

4. RMSProp

也是一种自适应学习率方法，是AdaDelta方法的变体，也是AdaGrad方法的一种发展，主要解决AdaGrad下降过快的问题。

AdaGrad方法会累加之前所有的梯度平方，而RMSProp方法只是计算此前梯度的均方根值。

该方法适合处理非平稳目标，对于RNN效果很好。

5. Adam

Adaptive Momentum Estimation，基本上是在RMSProp方法的基础上增加了动量：

\[m_t = \mu * m_{t-1} + (1 - \mu) * g_t\] \[n_t = \nu * n_{t-1} + (1 - \nu) * g^2_t\] \[\hat{m_t} = \frac{m_t}{1 - \mu^t}\] \[\hat{n_t} = \frac{n_t}{1 - \nu^t}\] \[\Delta\theta_t = - \frac{\hat{m_t}}{\sqrt{\hat{n_t}} + \epsilon} * \eta\]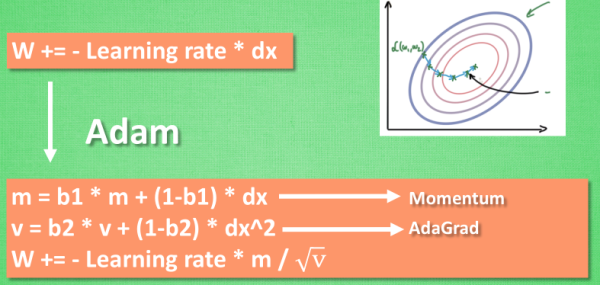

动量$\rightarrow$为梯度下降提供了“惯性动力”
AdaGrad$\rightarrow$为梯度下降带来了阻力

附：对比

第一张图为不同算法在损失平面等高线上随时间的变化情况，第二张图为不同算法在鞍点处的行为比较。

TensorFlow原生提供了多种优化器:

class tf.train.GradientDescentOptimiazer

class tf.train.AdadeltaOptimizer

class tf.train.AdagradOptimizer

class tf.train.AdagradDAOptimizer

class tf.train.AdamOptimizer

class tf.train.FtrlOptimizer

class tf.train.MomentumOptimizer

class tf.train.ProximalAdagradOptimizer

class tf.train.ProximalGradientDescentOptimizer

class tf.train.RMSPropOptimizer

class tf.train.sdca_optimizer

class tf.train.SyncReplicasOptimizer